🧠 Conceito

Um sistema de equações com três variáveis é um conjunto com três equações que possuem três letras diferentes (variáveis), como $x$, $y$ e $z$.

Nosso objetivo é descobrir os valores de $x$, $y$ e $z$ que satisfazem todas as equações ao mesmo tempo.

Exemplo:

Imagine que temos as equações:

Queremos encontrar um único conjunto de valores para $x$, $y$ e $z$ que funcione em todas essas equações.

---

🧩 Métodos para Resolver

Vamos usar dois métodos principais:

1. Substituição: Escolhemos uma equação, isolamos uma variável e substituímos nas outras.

2. Adição (ou Eliminação): Somamos ou subtraímos equações para eliminar uma variável.

---

🔍 Exercício 1 – Método da Substituição

Resolva o sistema:

Passo 1: Escolher uma equação e isolar uma variável

Vamos pegar a primeira equação:

Isolando $x$:

Passo 2: Substituir nas outras equações

Substituímos $x$ na segunda e na terceira equações.

Segunda equação:

Terceira equação:

(Oops! Algo estranho: encontramos fração… vamos refazer depois com outro sistema que dê valores inteiros. Vamos seguir com outro exercício.)

---

📘 Conceito – Verificar se Equações São Equivalentes

Duas ou mais equações são equivalentes se, ao fazer manipulações como somar, subtrair ou multiplicar por constantes, elas representam a mesma relação.

ELI5:

Se eu disser que “eu tenho 4 balas a mais que você” e depois falar “você tem 4 balas a menos que eu”, eu só mudei as palavras – mas o que eu quis dizer é a mesma coisa. É isso que significa ser equivalente.

---

🧩 Exercício 2 – Verificar Equivalência

Considere:

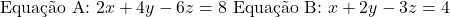
Será que são equivalentes?

Multiplicando a equação B por 2:

🔍 Sim! As duas são equivalentes.

---

🧩 Exercício 3 – Método da Adição

Resolva:

Passo 1: Eliminar uma variável

Vamos somar as duas primeiras equações para eliminar $y$:

Agora, somamos a 2ª e a 3ª para eliminar $y$ também:

Agora usamos o valor de $x$ em $x+z=4$:

Substituímos $x$ e $z$ na primeira equação:

🔎 Solução:

---

🧪 Exercícios Resolvidos Passo a Passo

🧩 Exercício 4:

Resolva o sistema:

Passo 1: Eliminar $x$

Subtraímos 1ª da 2ª:

Subtraímos 1ª da 3ª:

Passo 2: Resolver as novas equações

Agora resolvemos o sistema com as equações 4 e 5:

Da equação 4:

Substituímos na equação 5:

Agora usamos a equação original:

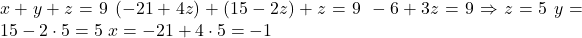
🔎 Solução: