Exercício 1

Se $x$ e $y$ são grandezas inversamente proporcionais, e sabemos que $x=4$ quando $y=6$, determine o valor de $y$ quando $x=8$.

Resolução:

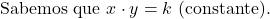
1. Substitua os valores iniciais de $x$ e $y$ para encontrar $k$:
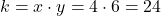
2. Agora, use a mesma constante $k=24$ para encontrar $y$ quando $x=8$:

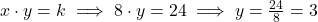
Resposta: $y=3$

---

Exercício 2

Duas grandezas $A$ e $B$ são inversamente proporcionais. Se $A=10$ quando $B=5$, qual é o valor de $A$ quando $B=2$?

Resolução:

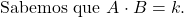
1. Encontre a constante $k$ usando os valores iniciais:
2. Use $k=50$ para encontrar $A$ quando $B=2$:

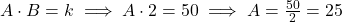
Resposta: $A=25$

---

Exercício 3

Um carro percorre uma distância fixa. Se ele viaja a $60\text{km/h}$, leva $4\text{horas}$. Quanto tempo levará se a velocidade for $80\text{km/h}$?

Resolução:

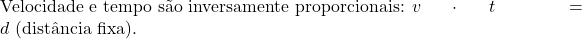
1. Calcule a distância total:
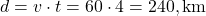
2. Use a mesma distância para encontrar o tempo $t$ quando $v=80\text{km/h}$:

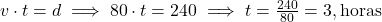
Resposta: $t=3\text{horas}$

---

Exercício 4

Se $x$ e $y$ são inversamente proporcionais, e $x=5$ quando $y=12$, calcule $x$ quando $y=15$.

Resolução:

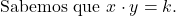
1. Encontre a constante $k$:
2. Use $k=60$ para encontrar $x$ quando $y=15$:

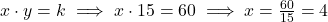
Resposta: $x=4$

---

Exercício 5

Um pedreiro constrói uma parede em $12\text{dias}$ trabalhando $8\text{horas/dia}$. Quantos dias levará se trabalhar $6\text{horas/dia}$?

Resolução:

1. Calcule a constante $c$:
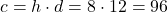
2. Use $c=96$ para encontrar $d$ quando $h=6$:

Resposta: $d=16\text{dias}$

---

Exercício 6

Se $m$ e $n$ são inversamente proporcionais, e $m=7$ quando $n=9$, calcule $n$ quando $m=21$.

Resolução:

1. Encontre a constante $k$:
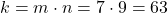
2. Use $k=63$ para encontrar $n$ quando $m=21$:

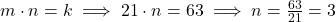
Resposta: $n=3$

---

Exercício 7

Um grupo de operários conclui uma obra em $15\text{dias}$ trabalhando $8\text{horas/dia}$. Quantas horas por dia eles precisarão trabalhar para terminar a obra em $10\text{dias}$?

Resolução:

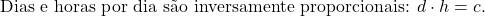
1. Calcule a constante $c$:
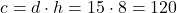
2. Use $c=120$ para encontrar $h$ quando $d=10$:

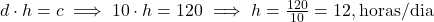
Resposta: $h=12\text{horas/dia}$

---

Exercício 8

Se $p$ e $q$ são inversamente proporcionais, e $p=12$ quando $q=4$, calcule $p$ quando $q=6$.

Resolução:

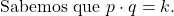
1. Encontre a constante $k$:
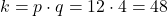
2. Use $k=48$ para encontrar $p$ quando $q=6$:

Resposta: $p=8$

---

Exercício 9

Uma torneira enche um tanque em $6\text{horas}$. Quantas torneiras iguais serão necessárias para encher o mesmo tanque em $2\text{horas}$?

Resolução:

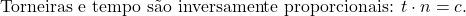
1. Calcule a constante $c$:
2. Use $c=6$ para encontrar $n$ quando $t=2$:

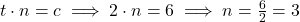
Resposta: $n=3\text{torneiras}$

---

Exercício 10

Se $r$ e $s$ são inversamente proporcionais, e $r=15$ quando $s=3$, calcule $s$ quando $r=5$.

Resolução:

1. Encontre a constante $k$:
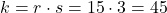
2. Use $k=45$ para encontrar $s$ quando $r=5$:

Resposta: $s=9$