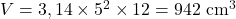📚 Conceitos Fundamentais
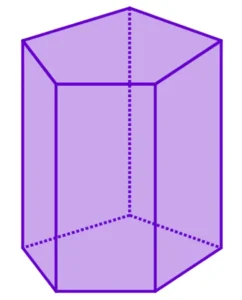
🔷 Prisma Reto
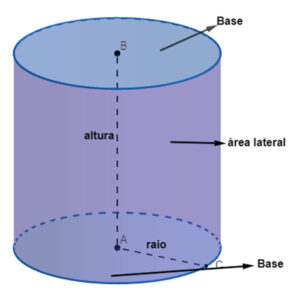
🟠 Cilindro Reto
🧮 Exemplos Resolvidos
Exemplo 1: Prisma Reto de Base Retangular
Problema: Calcular o volume de um prisma reto com base retangular de 5 cm por 3 cm e altura de 10 cm.
Solução:
Área da base:

Volume:
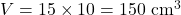
Resposta: 150 cm³.
Exemplo 2: Cilindro Reto
Problema: Calcular o volume de um cilindro com raio de 4 cm e altura de 12 cm.
Solução:
Volume:

Resposta: 602,88 cm³.
📝 Exercícios Propostos
🟦 Prismas Retos
-
Calcular o volume de um prisma reto cuja base é um triângulo com lados de 6 cm, 8 cm e 10 cm, e altura de 18 cm.
-
Um prisma reto tem base hexagonal regular com lado de 2 cm e apótema de 1,73 cm, e altura de 25 cm. Calcular seu volume.
-
Calcular o volume de um prisma reto com base quadrada de lado 10 cm e altura de 15 cm.
-
Calcular o volume de um prisma reto com base retangular de 7 cm por 5 cm e altura de 20 cm.
-
Calcular o volume de um prisma reto cuja base é um triângulo equilátero de lado 6 cm e altura de 10 cm.
🟨 Cilindros Retos
-
Calcular o volume de um cilindro com raio de 5 cm e altura de 10 cm.
-
Calcular o volume de um cilindro com diâmetro de 8 cm e altura de 15 cm.
-
Calcular o volume de um cilindro com raio de 3 cm e altura de 20 cm.
-
Calcular o volume de um cilindro com raio de 7 cm e altura de 14 cm.
-
Calcular o volume de um cilindro com diâmetro de 10 cm e altura de 12 cm.
✅ Gabarito
Prismas Retos
1. Prisma Triangular:
Área da base:
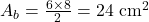
Volume:
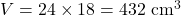
2. Prisma de Base Hexagonal:
Perímetro da base:

Área da base:
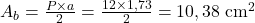
Volume:

3. Prisma de Base Quadrada:
Área da base:
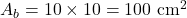
Volume:

4. Prisma de Base Retangular:
Área da base:

Volume:

5. Prisma de Base Triangular Equilátera:
Área da base:

Volume:
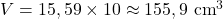
Cilindros Retos
6. Cilindro com Raio e Altura Dados:
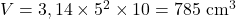
7. Cilindro com Diâmetro e Altura Dados:
Raio:

Volume:
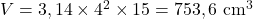
8. Cilindro com Raio e Altura Dados:
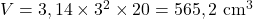
9. Cilindro com Raio e Altura Dados:
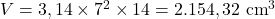
10. Cilindro com Diâmetro e Altura Dados:
Raio:
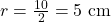
Volume: